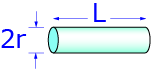
Cylinder
(L>>r)
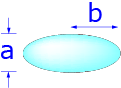
Ellipsoid
(b>>a)

水溶液中の微小物体の粘性抵抗係数について考えていきましょう.
水溶液中で微小物体であるので,基本的には小さなレイノルズ数の場合を扱いますので,基本的には,
ストークスの法則に従う
乱流などを考慮しない
場合を考えます.
また,私の力量ではストークスの法則自体を解くことができませんので,各文献を調べて,各形状による粘性抵抗係数の考え方を考えていきたいと思います.
J. Howardの著書,”Mechanics of Motor Proteins and the Cytoskeleton”によると
\(\Large \hspace{ 60pt} \gamma_{ \parallel } \hspace{ 150pt } \gamma_{ \perp } \hspace{ 150pt } \gamma_r \)
| Parameter | Direction | Cylinder |
Ellipsoid |
Sphere |
 |
 |
 |
||
| \(\Large \gamma_{ \parallel }\) | |
\(\Large \frac{2 \pi \eta L}{ln(L/(2r))-0.20} \) | \(\Large \frac{4 \pi \eta b}{ln((2b)/a)-0.5} \) | \(\Large 6 \pi \eta r \) |
| \(\Large \gamma_{ \perp } \) |  |
\(\Large \frac{4 \pi \eta L}{ln(L/(2r))+0.84} \) | \(\Large \frac{8 \pi \eta b}{ln((2b)/a)+0.5} \) | \(\Large 6 \pi \eta r \) |
| \(\Large \gamma_r \) |  |
\(\Large \frac{ \frac{1}{3} \pi \eta L^3}{ln(L/(2r))-0.66} \) | \(\Large \frac{ \frac{8}{3} \pi \eta b}{ln((2b)/a)-0.5} \) | \(\Large 8 \pi \eta r^3 \) |
| \(\Large \gamma_a \) | |
\(\Large 4 \pi \eta r^2 L\) | \(\Large \frac{16}{3} \pi \eta a^2 b \) | \(\Large 8 \pi \eta r^3 \) |
ここで注意すべき点は,
Cylinder (L>>r)
Ellipsoid (b>>a)
とあるように,かなり細長い(アスペクト比の高い)形状でしか成り立たない式と言うことです.
では,L≒r,b≒a,の場合にこの式を使うとどうなるかを考えてみましょう.